P1866 编号

题目描述

太郎有 $N$ 只兔子，现在为了方便识别它们，太郎要给他们编号。兔子们向太郎表达了它们对号码的喜好，每个兔子 $i$ 想要一个整数，介于 $1$ 和 $M_i$ 之间（可以为 $1$ 或 $M_i$）。当然，每个兔子的编号是不同的。现在太郎想知道一共有多少种编号的方法。
你只用输出答案对 $10^9+7$ 取余的结果即可。如果这是不可能的，就输出 $0$。

输入格式

第一行是一个整数 $N$。
第二行 $N$ 个整数 $M_i$。

输出格式

一个整数，表示方案总数。

样例 #1

样例输入 #1

1
2
2
5 8

样例输出 #1

1
35

提示

数据范围及约定

对于全部数据，$1 \le N \le 50$，$1\le M_i\le 1000$。

题解

分析

  • 排列组合，可以推出结果
  • 每个兔子拿到的数字都不能相同，说明第一个兔子如果选择了1，第二个就不能选1了，我们可以从小到大排列

wtf

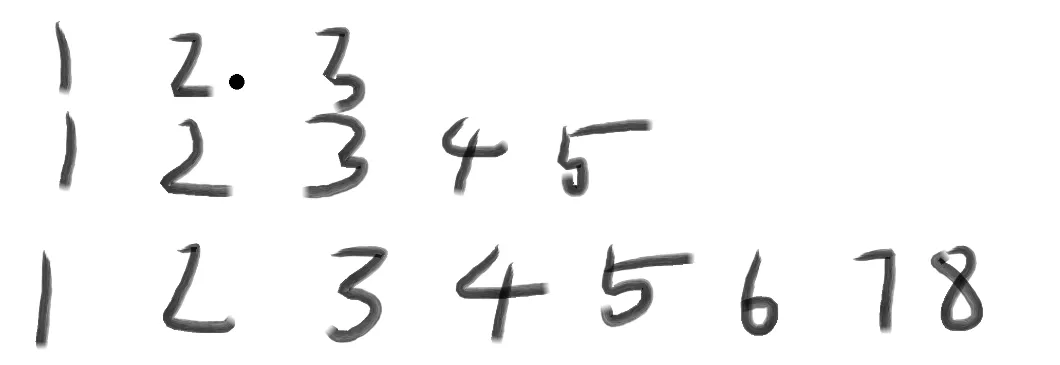
这组数据就为3 5 8
我们拿取他们的数字，于是就有 $C_{3}^{1}C_{5-1}^{1}C_{8-2}^{1}=C_{3}^{1}C_{4}^{1}C_{6}^{1} = 72$
以此可得 ${\textstyle \prod_{i=0}^{n} (M_{i}-(i+1))}$

解释

  • 0处的最小的数先选$M_{0}$，于是能够选择的个数有$C_{M_{0}}^{1}$种
  • 1处的数字开始选择,因为上一个比他小或者等于他的数列选择过了一次，所以只能选择 $M_1 - 1$个数字了
  • 2处 能够选择的数只有$M_{2}-2$个
  • …
  • 以此类推就有了上面的公式($i$是从0开始所以需要+1，如果要像下面的代码一样则需要从 1 开始循环)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.io.*;
import java.math.BigInteger;
import java.util.Arrays;

public class P1866 {

    public static void main(String[] args) throws Throwable {
        int n = nextInt();

        int[] arr = new int[n];
        // 输入数据
        for (int i = 0; i < n; i++) arr[i] = nextInt();
        // nlogn 排序
        Arrays.sort(arr);
        // 预先存入arr[0]的数据
        // 用BigInteger防止数据爆炸
        BigInteger sum = BigInteger.valueOf(arr[0]);
        // 从1开始循环
        for (int j = 1; j < arr.length; j++) {
            sum = sum.multiply(BigInteger.valueOf(arr[j] - j));
        }
        pw.println(sum.mod(BigInteger.valueOf((long) (1e9 + 7))));
        pw.flush();
    }

    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    // 快读
    public static int nextInt() throws Throwable {
        st.nextToken();
        return (int) st.nval;
    }
}